这里是暑假数学一轮笔记。
随便写写的,会写点二级结论、例题和证明。
可能为了连贯会写非常水的,也会写非常难的。(写完后发现按照编排恰好难度大致递增)
不一定是从书上抄来的,有些可能是我个人想到的 idea。
例题一般只有 做法极其经典 或 我的做法比标准答案简单 或 解法极具启发意义 我才会写解法。
这篇笔记的目的是介绍各种好用的思想方法和难推且好用的结论(主要在解析几何部分。实际上,这部笔记原本就是为了解析几何的大量二级结论而写的)不要把所有的结论都记住,这不是这篇笔记的目的。对于能快速推导的结论,应该从阅读这篇笔记中锻炼思维,从而掌握推导过程,每次用的时候现推。把所有的东西都记住只会让自己变傻。做题最重要的是脑子,结论只能在有脑子的前提下起辅助作用,千万不要满脑子只有结论。
不一定会按照高中数学课本的规范写公式和术语。
不要外传给任何人,因为我觉得这个拿出去卖钱能挣一大笔,并且这个排版太丑,拿出去很丢人。
所有蓝色的超链接都是能点的(
[TOC]
三角函数
由于复习的时候不在暑假所以没想到写啥,实际上三角函数也没啥结论,全是公式。
已知扇形的周长为 $C$,则面积 $S = \frac{C^2}{2( \alpha + \frac 4 \alpha + 4)}$,其中 $\alpha$ 为圆心角。当 $\alpha = 2 \ \mathrm{rad}$ 时,$S_{\max} = \frac{C^2}{16}$。
$a\sin x + b\cos x = \sqrt{a^2 + b^2} \sin(x + \varphi)$,其中 $\tan \varphi = \frac ba$。虽然辅助角公式已经记烂了,但还是写一下表示尊重。
用 $\tan \alpha$ 表示 $\sin 2\alpha, \ \cos 2\alpha, \ \tan 2\alpha$ 的式子可以先降一次幂然后除以 $\sin^2 \alpha + \cos^2 \alpha$ 再瞎比 $\cos \alpha$ 得到。这个的用处主要是推导过程,公式太乱就不打了。
在 $\triangle ABC$ 中,由于 $A + B < \pi$ 的限制,$A < B \Longleftrightarrow \sin A < \sin B$。
噔噔咚 和差化积、积化和差
平面向量
向量属实是又简单又好用的玩意了。
对于起点相同、终点共线的三个向量 $\vec{ON}, \vec{OP}, \vec{OQ}$($O$ 与 $PQ$ 不共线),总有 $\vec{ON} = u \cdot \vec{OP} + v \cdot \vec{OQ}$,其中 $u + v = 1$。
例 设两个非零向量 $\vec a$ 与 $\vec b$ 不共线,若 $\vec a$ 与 $\vec b$ 的起点相同,且 $\vec a, t \vec b, \frac 13( \vec a + \vec b)$ 的终点在同一条直线上,求实数 $t$ 的值。
解 设 $\begin{cases} \frac 13( \vec a + \vec b) = u \vec a + vt \vec b \\ u + v = 1 \end{cases}$,解出来就完事🌶
在上一条的基础上,如果有 $\vec{OM} = \lambda \vec{ON}$,则有 $\vec{OM} = u \cdot \vec{OP} + v \cdot \vec{OQ}$,其中 $u + v = \lambda$。有很多题可以用这个简化。
若 $G$ 为 $\triangle ABC$ 的重心(中线的交点),则有 $\vec{GA} + \vec {GB} + \vec {GC} = 0 $,$\vec{AG} = \frac 13( \vec{AB} + \vec{AC})$。
- 这个结论在立体几何那章的题目里会非常有用:设正三角形的边长为 $a$,则某个顶点到重心的距离为 $\frac{ \sqrt 3}3 a$。相应地,重心到某条边的距离为 $\frac{ \sqrt 3}6 a$。
复数
复数相乘,模相乘,幅角相加;复数相除,模相除,幅角相减。
- 记住这个看起来非常 naive 的结论,脑子里再带着个复平面,大部分复数题可以秒出。
例 复数 $z = \frac {3 + 4i}{12 - 5i}$($i$ 为虚数单位),求 $|z|$。
解 分子模是 $5$,分母模是 $13$,完事了。[这里本来的那句话已注释掉]
数列
[这里本来的那句话已注释掉]
数列题大部分是比较需要脑子的,但也有少部分烂题会不会结论完全就是两种感受。
本节中默认 $n \in \N^\ast$,不再赘述。
求通项公式
这节没有值得学习的东西。一轮之后的阅读请跳过这节。
$a_n = \begin{cases} S_1 &, n = 1 \\ S_n - S_{n - 1} &, n \ge 2 \end{cases}$,写这条是为了提醒你求出通项不要忘记验证 $a_1$ 是否满足。
例 已知数列 $\{ a_n \}$ 的前 $n$ 项和公式为 $S_n = 2n^2 - n + 1$,求 $a_n$。
答案 $a_n = \begin{cases} 2 &, n = 1 \\ 4n - 3 &, n \ge 2 \end{cases}$
已知 $\frac{a_{n + 1}}{a_n} = f(n)$,求 $a_n$,上累乘。
例 1 已知在数列 $\{ a_n \}$ 中,已知 $a_1 = 1, na_{n - 1} = (n + 1)a_n \ (n \ge 2)$,求 $a_n$。
解
例 2 已知在数列 $\{ a_n \}$ 中,$a_1 = 2, (n + 2)a_{n + 1} - (n + 1)a_n = 0$,求 $a_n$。
答案 $a_n = \frac 4{n + 1}$
类似地,已知 $a_{n + 1} - a_n = f(n)$,上累加。
例 1 已知在数列 $\{ a_n \}$ 中,$a_1 = 2, a_n - a_{n - 1} = 3n - 1 \ (n \ge 2)$,求 $a_n$。
解
例 2 已知在数列 $\{ a_n \}$ 中,$a_1 = 2, a_{n + 1} = a_n + \frac 1{n(n + 1)}$,求 $a_n$。
答案 $a_n = 3 - \frac 1n$
已知 $a_{n + 1} = pa_n + q$,待定系数设 $a_{n + 1} + \lambda = p(a_n + \lambda)$,求出 $\lambda$,$\{ a_n + \lambda \}$ 是等比数列。
例 已知在数列 $\{ a_n \}$ 中,$a_1 = 3$,且点 $P_n(a_n, a_{n + 1})$ 在直线 $4x - y + 1 = 0$ 上,求 $a_n$。
解 发现 $a_{n + 1} = 4a_n + 1$。通过上面方法得到 $a_{n + 1} + \frac 13 = 4 \left(a_n + \frac 13 \right)$,则 $\left\{ a_n + \frac 13 \right\}$ 是首项为 $\frac{10}3$,公比为 $4$ 的等比数列。$a_n = \frac 56 \cdot 4^n - \frac 13$。
剩下的求通项题就比较人类智慧了。比如这个(?)
等差数列相关
本节中默认 $\{ a_n \}$ 是首项为 $a_1$,公差为 $d$ 的等差数列,$S_n$ 为其前缀和。
若 $a, b, c$ 成等差数列,即 $b$ 是 $a$ 和 $c$ 的等差中项,则 $2b = a + c$。其实就是算术平均数。
$a_n = a_m + (n - m)d$
$S_n = \frac{n(a_1 + a_n)}2 = na_1 + \frac{n(n - 1)}2 d$
- $\left \{ \frac{S_n}n \right \}$ 也是等差数列,$\frac{S_n}n = a_1 + \frac{n - 1}2 d$。
$S_n, S_{2n - n}, S_{3n - 2n}, \cdots$ 成等差数列,公差为 $n^2d$。
若项数为偶数 $2n$,则 $S_{2n} = n(a_1 + a_{2n}) = n(a_{n} + a_{n + 1})$,$\frac{S_{ \text{even}}}{S_{ \text{odd}}} = \frac{a_n}{a_{n + 1}}$。
若项数为奇数 $2n - 1$,则 $S_{2n - 1} = (2n - 1)a_n$,$S_{ \text{odd}} - S_{ \text{even}} = a_n$,$\frac{S_{ \text{odd}}}{S_{ \text{even}}} = \frac{n}{n - 1}$。
- 校对过了,上两条不对称的地方没有错误。证明都不难,直接套通项就行,难就难在第一个想出这些结论。
若数列 $\{ a_n \}$ 和 $\{ b_n \}$ 均为等差数列,且前 $n$ 项和分别是 $S_n$ 和 $T_n$,则 $\frac{S_{2m - 1}}{T_{2m - 1}} = \frac{a_m}{b_m}$。
等比数列相关
本节中默认 $\{ a_n \}$ 是首项为 $a_1$,公比为 $q \ (q \ne 0)$ 的等比数列,$S_n$ 为其前缀和,$T_n$ 为其前缀积。
若 $a, b, c$ 成等比数列,即 $b$ 是 $a$ 和 $c$ 的等比中项,则 $b^2 = ac$(反之不能推出,因为可能出现 $0$)。其实就是几何平均数。
$a_n = a_m q^{n - m}$
若 $q \ne 1$,$S_n = \frac{a_1(1 - q^n)}{1 - q} = \frac{a_1 - a_n q}{1 - q}$。
$T_n = (a_1 a_n)^{ \frac n2} = a_1^n q^{ \frac{n(n - 1)}2}$
若 $q \ne -1$,$S_n, S_{2n} - S_n, S_{3n} - S_{2n}, \cdots$ 成等比数列,公比为 $q^n$。
$T_n, \frac{T_{2n}}{T_n}, \frac{T_{3n}}{T_{2n}}, \cdots$ 成等比数列,公比为 $q^{n^2}$。
若项数为奇数 $2n + 1$,则 $T_{2n + 1} = a_n^{2n + 1}$。
- 不光这个,显然上面等差数列前缀和对原数列的减法性质和做等比数列对原数列的除法性质是一一对应的。虽然非常简单,但是做题想不到就会像吃屎一样难受。
$S_{n + m} = S_n + q^n S_m = S_m + q^m S_n$
例 已知数列 $\{ a_n \}$ 是各项都为正数的等比数列,$S_n$ 为其前 $n$ 项和,且 $S_{10} = 10, S_{30} = 70$,求 $S_{40}$。
解 $30$ 是 $10$ 的整数倍,所以可以拆成 $S_{10}(1 + q^{10} + q^{20}) = S_{30}$,解得 $q^{10} = 2$(另一根舍去)。就可以用这个非常显然的结论了。例如,$S_{40} = S_{10} + q^{10} S_{30}$,等号右面的三项都已知。
数列求和
这节没有值得学习的东西。一轮之后的阅读请跳过这节。
等差数列求和公式:$S_n = \frac{n(a_1 + a_n)}2 = na_1 + \frac{n(n - 1)}2 d$。
等比数列求和公式:$S_n = \begin{cases} na_1 &, n = 1 \\ \frac{a_1(1 - q^n)}{1 - q} = \frac{a_1 - a_n q}{1 - q} & , n \ne 1 \end{cases}$。
倒序相加
适用于序列自身循环卷积后非常好算的情况。例如用于等差数列求和公式的推导。
分组求和
其实就是加法结合律。例如求 $a_n = 2^n + n$ 的前缀和。
并项求和
其实也是加法结合律。例如求 $a_n = (-1) f(n)$ 的前缀和,可以把奇偶项分别求和再相加。
错位相减
适用于等于等差数列乘以等比数列的数列求和,当然也可以推导等比数列求和公式。例如求 $a_n = n \cdot 2^n$ 的前缀和。
裂项相消
把数列的通项拆成两项之差,在和式中某些项可以相互抵消,从而求得和。见裂项公式。
立体几何
这一块太水的东西就不写了。像什么长方体边长和内切球、外切球半径的关系,正四棱锥边长和表面积、体积、内切球外接球半径的关系之类的,瞎推就能出来,都写了没意思,当成结论记对脑子也不好。
后半段能用向量做的题也不会有啥结论值得学,有用的东西应该都会写在题目部分。
棱锥和球
经常会有题目把棱锥和球(内切球、外接球)联系起来(比如 2019 全国 I 卷 T12)。
有些把棱锥放进外接球的题目,可以把棱锥放进长方体来更方便地求出球外接球的半径。
- 详见小题题第二题。
- 当然更多的题棱锥自身性质放不进长方体里,这样就只能勾股定理爆算了。
对于把内切球放进棱锥的题目,可以通过其体积 $V$ 和表面积 $S$ 来更方便地求出内切球球的半径 $r$:$\frac 13 Sr = V$。
- 这个式子的意义考虑把棱锥分割成若干个以内切球半径为高的三棱锥一并求出体积。
球心与任意一个截面圆圆心的连线垂直于截面圆。经常由此性质确定球心的位置。
点、直线和平面
多看几遍也不错
- 公理
- 如果一条直线上的两点在同一个平面内,那么这条直线在此平面内。
- $A \in l, B \in l, A \in \alpha, B \in \alpha \Longrightarrow l \in \alpha$
- 过不在同一条直线上的三点,有且只有一个平面。
- 过一条直线和这条直线外一点有且只有一个平面。
- 过两条相交直线有且只有一个平面。
- 过两条平行直线有且只有一个平面。
- 如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线。
- $P \in \alpha, P \in \beta \Longrightarrow \alpha \cap \beta = l, P \in l$
- 平行于同一条直线的两条直线互相平行。
- $a \parallel b, a \parallel c \Longrightarrow b \parallel c$
- 如果一条直线上的两点在同一个平面内,那么这条直线在此平面内。
- 过平面外一点和平面内一点的直线与平面内不过该点的直线是异面直线。
不等式
均值不等式
设 $x_1, x_2, \cdots, x_n \in \R_+$,则
当且仅当 $x_1 = x_2 = \cdots = x_n$ 时取等号。
证明
$n = 1$ 时显然成立。
引理:$\forall a, b \in \R_+, \frac 12(a + b) \ge \sqrt{ab}$,当且仅当 $a = b$ 时取等号。引理的证明通过基本不等式 $\forall a, b \in R, a^2 + b^2 \ge 2ab$。当 $a, b \ge 0$ 时以 $\sqrt a, \sqrt b$ 取代 $a, b$。这样就证明了 $(1)$ 式当 $n = 2$ 时成立。
考虑数学归纳法。若 $n = k \ (k \ge 2)$ 的情况成立,对于 $n = k + 1$ 的情况,考虑将 $(1)$ 式左右分别提出前 $k$ 项的和或积,故而 $n = k + 1$ 的情况也成立。$\square$
柯西不等式
设 $a_1, a_2, \cdots, a_n, b_1, b_2, \cdots, b_n \in \R$,则
等号成立条件:$\frac{a_1}{b_1} = \frac{a_2}{b_2} = \cdots = \frac{a_n}{b_n}$,或 $b_i = 0$。
证明
令 $f_i(x) = (a_i x + b_i)^2$,则 $f(x) = \sum_{i = 1}^n{f_i(x)} \ge 0$。因此其判别式 $\Delta = 4 \left( \sum_{i = 1}^n{x_i y_i} \right)^2 - 4 \left( \sum_{i = 1}^n{x_i^2} \right) \left( \sum_{i = 1}^n{y_i^2} \right) \le 0$。化简即得柯西不等式。$\square$
当然也可以用向量证。
二维形式
推广形式
推论
小于方向
大于方向
推论 - 权方和不等式
排序不等式
设 $a_1 \le a_2 \le \cdots \le a_n, \ b_1 \le b_2 \le \cdots \le b_n$,$\{c_n\}$ 是 $\{b_n\}$ 的一个排列。若
则有 $S_1 \le S_3 \le S_2$。
其他的不等式
设 $x_1, x_2, \cdots, x_n \in \R_+$,则
证明:不等式两边同时加上不等式右边,原命题转化为证 $\frac{x_1^2}{x_2} + x_2 \ge 2x_1$(当且仅当 $x_1 = x_2$ 时取等号),其他各项同理。而这个不等式的正确性是显然的(通过基本不等式)。$\square$
杂项
裂项公式
- $\frac 1{n(n + k)} = \frac 1k \left( \frac 1n - \frac 1{n + k} \right)$
$\frac 1{(2n - 1)(2n + 1)} = \frac 12 \left( \frac 1{2n - 1} - \frac1{2n + 1} \right)$
- 上两条其实是一个一般公式的特殊情况。
- 若 $\{ a_n \}$ 是公差为 $d$ 的等差数列,则 $\frac 1{a_n a_{n + 1}} = \frac 1d \left( \frac 1{a_n} - \frac 1{a_{n + 1}} \right)$。
$\frac{2^n}{(2^n + 1)(2^{n + 1} + 1)} = \frac{1}{2^n + 1} - \frac{1}{2^{n + 1} + 1}$
- $\frac{x^n}{(x^n + k)(x^{n + 1} + k)} = \frac 1{x - 1} \left( \frac{1}{x^n + k} - \frac{1}{x^{n + 1} + k} \right)$
$\frac 1{n(n + 1)(n + 1)} = \frac 12 \left( \frac 1{n(n + 1)} - \frac 1{(n + 1)(n + 2)} \right)$
- $\frac 1{ \sqrt n - \sqrt{n + k}} = \frac 1k( \sqrt{n + k} - \sqrt n)$
和式
- $\sum_{i = 1}^n{i^2} = \frac{n(n + 1)(2n + 1)}6$
- $\sum_{i = 1}^n{i^3} = \left( \frac{n(n + 1)}2 \right)^2$
不等式
- $e^x \ge x + 1$,当且仅当 $x = 0$ 时取等号。
- $e^x \ge ex$,当且仅当 $x = 1$ 时取等号。
- $\ln x \le x - 1$,当且仅当 $x = 1$ 时取等号。
- $\ln x \ge 1 - \frac 1x$,当且仅当 $x = 1$ 时取等号。
其他
- 立方和差公式:$a^3 \pm b^3 = (a \pm b)(a^2 \mp ab + b^2)$
- 已知 $f(x)$ 是定义在 $\R$ 上的函数:
- 若 $f(a + x) = f(b - x)$ 恒成立,则 $y = f(x)$ 的图像关于直线 $x = \frac{a + b}2$ 对称。
- 若 $f(a + x) + f(a - x) = 0$ 恒成立,则 $y = f(x)$ 的图像关于点 $(a, 0)$ 中心对称。
- 若 $y = f(x)$ 有两条对称轴 $x = a, \ x = b$,则 $y = f(x)$ 为周期函数,且一个周期为 $2|b - a|$。
小题题
有一堆不等式杂题在隔壁这个文件。
(多选)已知曲线 $C: y^2 = 2x + a$ 在点 $P_n(n, \sqrt{2n + a}) \ (a > 0, n \in \N)$ 处的切线 $l_n$ 的斜率为 $k_n$,直线 $l_n$ 交 $x$ 轴、$y$ 轴分别于点 $A_n(x_n, 0)$、$B_n(0, y_n)$,且 $|x_0| = |y_0|$。以下结论中,正确的结论有()。
A. $a = 1$
B. 当 $n \in \N^\ast$ 时,$y_n$ 的最小值为 $\frac{2 \sqrt 3}3$
C. 当 $n \in \N^\ast$ 时,$k_n > \sqrt 2 \sin \frac 1{ \sqrt{2n + 1}}$
D. 当 $n \in \N^\ast$ 时,记数列 $k_n$ 的前 $n$ 项和为 $S_n$,则 $S_n < \sqrt 2( \sqrt{n + 1} - 1)$
答案 ABD。虽然是个大杂烩,但是题确实挺牛逼的。
因为 $P_n$ 的纵坐标 $\sqrt{2n + a} \ge 0$,所以可以只考虑 $y \ge 0$ 的情况,即 $y = \sqrt{2x + a}$。则 $y’ = \frac 1{ \sqrt{2x + a}}$,即 $k_n = \frac 1{ \sqrt{2n + a}}$。得 $C$ 在 $P_n$ 处的切线为 $y - \sqrt{2n + a} = \frac 1{ \sqrt{2n + a}} (x - n)$。则有 $x_n = -n - a, \ y_n = \frac{n + a}{ \sqrt{2n + a}}$。
A:把 $|x_0| = |y_0|$ 代入得 $|-a| = \left| \frac a{\sqrt a} \right|$,即 $a = 1$,A 正确。且有 $x_n = -n - 1, \ y_n = \frac{n + 1}{ \sqrt{2n + 1}}, \ k_n = \frac 1{ \sqrt{2n + 1}}$。
B:令 $t = \sqrt{2n + 1} \in [\sqrt 3, +\infty )$,代入推式子得 $y_n = \frac 12(t + \frac 1t)$。当 $t = \sqrt 3$ 时 $y_n$ 取最小值 $\frac{2 \sqrt 3}3$,B 正确。
C:令 $u = k_n = \frac 1t \in \left(0, \frac 1{ \sqrt 3} \right], \ v(u) = \sqrt 2 \sin u - u$,则 $v’(u) = \sqrt 2 \cos u - 1$。由 $0 < u \le \frac 1{ \sqrt 3} < \frac \pi 4$ 得 $v’(u) > 0$,即 $v(u)$ 在 $\left(0, \frac 1{ \sqrt 3} \right]$ 上单调增。$v(u) > v(0) = 0$,所以 $\sqrt 2 \sin u > u$ 恒成立,即 $k_n < \sqrt 2 \sin \frac 1{ \sqrt{2n + 1}}$,C 错误。
D:因为 $\left( \frac{a + b}2 \right)^2 \le \frac{a^2 + b^2}2$(当且仅当 $a = b$ 时取等号),所以 $a + b \le \sqrt{2(a^2 + b^2)}$。得到 $\sqrt n + \sqrt{n + 1} \le \sqrt 2 \cdot \sqrt{n + n + 1}$,从而 $\frac 1{ \sqrt{2n + 1}} < \frac{ \sqrt 2}{ \sqrt n + \sqrt{n + 1}} = \sqrt 2( \sqrt{n + 1} - \sqrt n)$。
D 正确。
- 已知正四面体 $A-BCD$ 的外接球的体积为 $8 \sqrt 6 \pi$,求这个四面体的表面积。
答案 $16 \sqrt 3$。
思路很明确。外接球的半径 $R = \sqrt 6$,接下来就是要想办法求出四面体的棱长。有两种方法。
把这个球画出来,用勾股定理暴力算。设棱长为 $a$,捣鼓半天可以列出这样一个式子:$( \sqrt 6)^2 = \left( \frac{ \sqrt 3}3 a \right)^2 + \left( \frac{ \sqrt 6}3 a - \sqrt 6 \right)^2$。
把这个三棱锥放在一个正方体里,如下图:
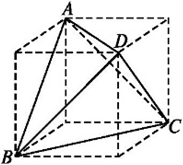
设正方体的边长为 $a$,则 $\sqrt 3 a = 2R$。又有棱锥的边长等于正方体的面对角线长 $\sqrt 2 a$。
两种方法都能得到棱锥的边长为 $4$,从而其表面积为 $16 \sqrt 3$。
这里有一个思想:把棱锥放进长方体,有时候会有意想不到的效果。
- 在三棱锥 $P-ABC$ 中,$AB = 5, \ BC = 3, \ CA = 4$。三个侧面与底面所成的角均为 $60^\circ$。求三棱锥的内切球的表面积。
答案 $\frac{4 \pi}3$。
首先底面是个直角三角形,可以求出它的内切圆的半径。底面内切圆半径、侧面三角形的高、棱锥的高组成的三角形已知一条边和两个角,可解。于是就得到了棱锥的表面积 $S$ 和体积 $V$。设 $r$ 为内切球半径,有 $\frac 13 Sr = V$。
(2017 全国 I 理数 T16)如图,圆形纸片的圆心为 $O$,半径为 $5$,该纸片上的等边三角形 $ABC$ 的中心为 $O$。$D, \ E, \ F$ 为圆 $O$ 上的点,$\triangle DBC, \ \triangle ECA, \ \triangle FAB$ 分别是以 $BC, \ CA, \ AB$ 为底边的等腰三角形,沿虚线剪开后,分别以 $BC, \ CA, \ AB$ 为折痕折起 $\triangle DBC, \ \triangle ECA, \ \triangle FAB$,使得 $D, \ E, \ F$ 重合,得到三棱锥。当 $\triangle ABC$ 的边长变化时,求所得三棱锥体积的最大值。
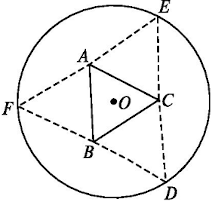
答案 $4 \sqrt{15}$。如图,连接 $OD$ 交 $BC$ 于点 $G$。
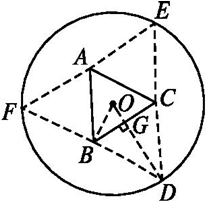
显然有 $OD \perp BC$。设 $OG = x$,则 $BC = 2 \sqrt 3 x, \ DG = 5 - x$。三棱锥的高 $h = \sqrt{DG^2 - OG^2} = \sqrt{25 - 10x}$。$V = \frac 13 Sh = \sqrt 3 \cdot \sqrt{25x^4 - 10x^5}$。令 $f(x) = 25x^4 - 10x^5 \ (0 < x < \frac 52)$,导数讨论可得 $f(x)_{ \max} = f(2) = 80$,从而当 $x = 2$ 时 $V_{ \max} = 4 \sqrt{15}$。
- 设 $a, b, c > 0$,求证:$\frac{(a + 1)^3}b + \frac{(b + 1)^3}c + \frac{(c + 1)^2}a \ge \frac{81}4$。
这是个轮换式,取等号时一定是三项相等,都等于 $\frac{27}4$。此时 $a = b = c = \frac 12$。利用这个可以进行构造。
证明:根据均值不等式,$\frac{(a + 1)^3}b + \frac{27}2 b + \frac{27}4 \ge 3 \sqrt[3]{ \frac{3^6 (a + 1)^3}{2^3}} = \frac{27(a + 1)}2$,当且仅当 $a = b = \frac 12$ 时取等号。其他两式同理。三式相加得到 $\mathrm{L.H.S.} + \frac{27}2(a + b + c) + \frac{81}4 \ge \frac{27}2(a + b + c) + \frac{81}2$。当且仅当 $a = b = c = \frac 12$ 时取等号。$\square$
这里 $\frac{(a + 1)^3}b + \frac{27}2 b + \frac{27}4$ 这三项是怎么来的呢…第一项是已知的对吧,我们要让它开三次根号,肯定要构造三项。我们已知三个数的值,并且要让构造出的三项都等于 $\frac{27}4$。因为这样最后三式相加,两边都是 $3 \times \frac{81}4$。
这里利用了均值不等式的添项方法。
- 设 $a, b, c > 0, \ a + b + c = 1$。求证:$\left(1 + \frac 1a \right) \left(1 + \frac 1b \right) \left(1 + \frac 1c \right) \ge 64$。
这个显然是 $a = b = c = \frac 13$ 时取等号。
证明:根据基本不等式,$1 + \frac 1a = 1 + \frac 1{3a} + \frac 1{3a} + \frac 1{3a} \ge 4 \sqrt[4]{ \frac 1{27a^3}}$,当且仅当 $a = \frac 13$ 时取等号。其他两式同理。三式相乘得到 $\mathrm{L.H.S.} \ge 64 \sqrt[4]{ \frac 1{3^9 a^3 b^3 c^3}}$,当且仅当 $a = b = c = \frac 13$ 时取等号。又有 $3 \sqrt[3]{abc} \le a + b + c = 1$,所以 $(abc)^3 \le \frac 1{3^9}$,当且仅当 $a = b = c = \frac 13$ 时取等号。$\square$
这里利用了均值不等式的拆项方法。